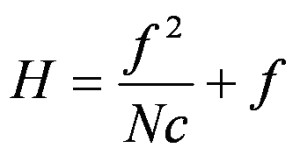La profondità di campo è delimitata da due piani, un piano posto tra la camera e il piano di messa a fuoco (posto a distanza Dn dalla camera) e un piano posto tra il piano di messa a fuoco e l’orizzonte (posto a distanza Df dalla camera). La distanza iperfocale H è quella distanza del soggetto a fuoco per la quale Df=infinito.

____________________

The depth of field is defined by a far Df limit plane and a near Dn limit plane. When we focus at a specific distance which corresponds a far limit equal to infinity,  we obtain the maximum depth of field. This specific distance is called hyperfocal distance.

 

Con:

f = lunghezza focale (mm),

N = apertura del diaframma (1.2,2,2.8,etc),

c = circolo di confusione (mm).

 

Come si vede dalla formula la distanza iperfocale è proporzionale al quadrato della lunghezza focale, ed è inversamente proporzionale all’apertura del diaframma e al circolo di confusione Dato che il circolo di confusione è costante per ogni fotocamera, per ogni apertura e lunghezza focale avremo quindi queste possibilità:

Distanza del soggetto a fuoco < H: man mano che il soggetto si allontana aumenta la profondità di campo, ma eventuali soggetti sullo sfondo a distanza ‘infinita’ non sono a fuoco.

Distanza del soggetto a fuoco = H: la profondità di campo va da Dn=H/2 fino a Df=infinito.  Ad esempio se voglio fotografare una persona davanti ad un panorama e voglio che sia la persona che il panorama siano a fuoco, la persona dovrà essere ad una distanza almeno pari a Dn=H/2 e dovrò impostare la messa a fuoco alla distanza H.

Distanza del soggetto a fuoco = infinito: man mano che sposto il fuoco da H ad infinito Dn tende ad H, con Df=infinito. Se in questo caso voglio fotografare una persona davanti ad un panorama, la persona dovrà essere ad una distanza almeno pari a Dn=H.

Vediamo il caso di un obiettivo da 24mm (CoC=0.013mm).

Se ad esempio sono sull’orlo di un precipizio e voglio fare una foto panoramica a mia moglie in una bella giornata di sole potrei impostare il diaframma a 16, mettere a fuoco a 2.8 metri e pormi ad una distanza da lei di 1.4 metri.  Se non andassimo molto d’accordo potrei lasciare anche il diaframma a 4, mettere a fuoco a 11.1 metri e chiederle di indietreggiare di 5.5 metri (si fa per scherzare!).

Per semplificarvi e semplificarmi la vita ho fatto questo semplice WIDGET per calcolare la distanza iperfocale.

Come è possibile vedere in questo articolo la posizione dei due piani Dn e Df che delimitano la profondità di campo dipende dalla distanza iperfocale. Maggiore è la distanza iperfocale, minore è la profondità di campo di un obiettivo e quindi maggiore è l’effetto sfuocato. Questo aspetto si dimostra molto utile quando vogliamo scegliere un obiettivo per fare un ritratto che abbia un bello sfondo sfuocato. Ad esempio: a parità di distanza del soggetto a fuoco, un obiettivo con un’iperfocale maggiore darà un effetto sfumato maggiore.

E’ analogamente interessante come lunghezze focali differenti e aperture del diaframma differenti che hanno la particolarità di avere la stessa distanza iperfocale, avranno la stessa profondità di campo e quindi lo stesso effetto sfuocato (ad esempio un 75mm F1.4, un 85mm F1.8, un 100mm F2.5 hanno circa la stessa iperfocale a 309 metri) anche se avranno inquadrature di ampiezza differente.

Se invece vogliamo mantenere lo stesso inquadramento (ingrandimento) e vogliamo vedere quale lente ci garantisce l’effetto sfumato migliore vai a questo articolo.

Se hai osservazioni, domande o dubbi, non esitare ad inserire un commento!

____________________

Circle of Confusion and Hyperfocal Distance

f = focal lenght (mm),

N = aperture (1.2,2,2.8,etc),

c = circle of confusion (mm).

 

If focus is set at a distance less than H the far limit of depth of field is not equal to infinity, so that the far background elements may not be in focus.

If focus is set at a distance equal to H the background elements are in focus and the near limit has a distance Dn=H/2 from the camera.

If focus is set equal to infinity the background elements are in focus, but the near limit has a distance Dn=H from the camera.

To make my life easyer I made this simple WIDGET  to calculate the hyperfocal distance.

The position of Dn and Df is related with the hyperfocal distance, so the bigger hyperfocal distance you have, the lower depth of field you get (read this post to understand this theme). If we focus at the same distance with two lenses, the one with the bigger hyperfocal distance will have a better bokeh. If we have two lenses with the same hyperfocal distance and we focus at the same distance they will have the same depth of field, but with different magnifications.

If you want to compare two lenses at the same magnification, in order to evaluate which ones has the biggest  bokeh, have a look to this post.

 

If you have any comments, questions or doubts, feel free to add a comment!
My English is not the best, if you find errors, help me to improve!